Curriculum für die Sekundarstufe I

Die folgenden schulinternen Unterrichtsinhalte sind obligatorisch bis auf die mit (E) gekennzeichneten Teile. Die fakultativen Inhalte werden jeweils dort aufgeführt, wo sie im Gefüge der Mathematik aus sachlogischen Gründen hingehören.

Aufgrund der Gestaltungsmöglichkeiten, die die Richtlinien von 1993 den Fachkonferenzen erlauben, sind alle wesentlichen Unterrichtsinhalte des Lernbereichs Stochastik in die Jahrgangsstufe 10 gelegt worden.

1. Natürliche Zahlen und ihre Darstellung

1.1 Große Zahlen / Vergleichen / Näherungswerte(Schätzen und Runden)

1.2 Der Zahlenstrahl

1.3 Dezimales Stellenwertsystem / Ziffern / Römische Zahlen /

ein weiteres Stellenwertsystem(z.B. Dualsystem)

2. Rechnen mit natürlichen Zahlen

2.1 Grundrechenarten mit Bezeichnungen / Rechengesetze mit

Rechenvorteilen / Vereinbarungen zur Klammerersparnis /

Schriftliches Rechnen und Kopfrechnen /Überschlagsrechnungen /

Anwendungen(Textaufgaben)

3. Einfache Größen

3.1 Geldwerte / Zeit / Längen / Massen

4. Gleichungen und mathematische Grundbegriffe

4.1 Aussagen und Aussageformen / einfache Gleichungen /

Mengenbegriffe: Vereinigungsmenge, Schnittmenge, Teilmenge, Restmenge

1. Körper und Netze

1.1 Herstellen und Zeichnen von Körpern(insbesondere Würfel, Quader)

1.2 Beschreibung von Pyramide, Tetraeder, Prisma, Zylinder, Kugel, Netze

2. Geometrische Grundbegriffe

2.1 Punkt, Strecke, Gerade, Halbgerade, Parallelität, Orthogonalität(Kon -

struktion mit Geodreieck), Abstand Punkt-Punkt und Punkt-Gerade(Lot)

3. Geometrische Figuren

3.1 Dreiecke / Vierecke / Kreise

4. Längen, - Flächen- und Rauminhalte

4.1 Umfang und Flächeninhalt von Rechtecken und Quadraten, Oberfläche

und Rauminhalt des Würfels und des Quaders

1. Teilbarkeit

1.1 Teiler und Vielfache / Teilbarkeitsregeln, Primzahlen,

Primfaktorzerlegung

1.2 ggT und kgV

2. Bruchzahlen

2.1 Bruchgrößen / Bruchzahlen

2.2 Kürzen - Erweitern - Anordnen von Bruchzahlen

2.3 Grundrechenarten und Rechengesetze

3. Dezimalzahlen

3.1                  Dezimalzahlen / Grundrechenarten / Runden / Überschlagsrech -
                        nungen /Anwendungen(relative Anteile als Anwendungen von Bruch -
                        und Dezimalzahlen, Prozentrechnung)

3.2                  Periodische Dezimalzahlen / Zahlenumwandlungen(periodische
                        Dezimalzahl¬® Bruchzahl)(kursorisch; nur einfache
                        Beispiele)

1. Geometrische Bewegungen

1.1 Verschiebung

1.2 Drehung / Winkel

1.3 Achsenspiegelung / Punktspiegelung

1.4 Konstruktion von Bildpunkten

1.5 Achsen -, Dreh -und Punktsymmetrie(kursorisch)

1.6 Verkettung von Spiegelungen und weiteren geometrischen Bewegungen (E)

Algebra(ab J-Stufe 7 ist der Einsatz eines Taschenrechners in das Ermessen der
FachlehrerInnen gestellt)

1. Rationale Zahlen

1.1                  Einführung der negativen Zahlen, der ganzen Zahlen und der
                        rationalen Zahlen / Zahlengerade / erweitertes Koordinatensystem /
                        Betrag einer Zahl

1.2 Rechnen mit rationalen Zahlen(Grundrechenarten, Rechengesetze,
Monotoniegesetze)

2. Funktionen

2.1 Zuordnung und Funktion / Darstellung der Zuordnungsvorschrift mit
Hilfe von Tabellen, Graphen und Termen

2.2 Proportionale und antiproportionale Zuordnungen

2.3 Anwendungen(Schluß -, Prozent -und Zinsrechnung)

1. Winkelsätze

1.1 Nebenwinkel / Scheitelwinkel / Stufenwinkel / Wechselwinkel /
Innenwinkelsummensatz im Dreieck

2. Kreis

2.1 Kreis und Geraden(Tangenten, Sekanten, Sehnen)

3. Winkel am Kreis

3.1 Der Satz des Thales

4. Vielecke

4.1 Gleichschenkliges, gleichseitiges und rechtwinkliges Dreieck,
Parallelogramm, Trapez, Rhombus

5. Besondere Linien im Dreieck

5.1 Höhe, Mittelsenkrechte, Umkreis, Winkelhalbierende, Inkreis,
Seitenhalbierende, Schwerpunkt(Konstruktion mit Zirkel und Lineal)

6. Kongruenz

6.1 Dreiecksgrundkonstruktionen, Kongruenzbegriff, Kongruenzsätze

1. Terme und Termumformungen

1.1 Anwendungen des Distributivgesetzes / Das Auflösen von
Klammern

2. Lösungsverf. für lineare Gleichungen und Ungleichungen

2.1 Einfache lineare Gleichungen

2.2 Einfache lineare Ungleichungen

2.3 Lineare Gleichungen mit Formvariablen(kurz!)

2.4 Textaufgaben

3. Der Funktionsbegriff

3.1                  Eindeutige Zuordnung und Funktionsbegriff / Übliche Begriffsbild. /
3.2                  Begriff der linearen Funktion / Definition der Steigung einer Gera -
                        den / Normalform der Geradengleichung / Berechnung der Schnitt -
‘                      punkte zweier Geraden / Betragsfunktion

4. Lineare Gleichungssysteme

4.1 Lineare Gleichungssysteme mit 2 Variablen(Einsetzungs -und
Additionsverfahren; auch für nicht eindeutig lösbare Systeme)

4.2                  Lineare Gleichungssysteme mit 3 Variablen(Beschränkung auf                          (E)
                        den eindeutig lösbaren Fall und rechnerisch einfach handhab-
                        bare Fälle)

4.3 Der Gaußsche Algorithmus(kursorisch!) (E)

5. Produkte und Potenzen von Summen

5.1 Umformung von Produkten in Summen und umgekehrt

5.2 Die Binomischen Formeln

6. Bruchterme

6.1 Definitionsmenge/ Multiplikation und Division von Bruchtermen

6.2 Das Dividieren einer Summe("Polynomdivision") (E)

1. Eigenschaften von Vielecken

1.1 Trapez, Parallelogramm, Raute und Drachen

1.2 Achsen -und punktsymmetrische Figuren

2. Flächeninhalte von Vielecken

2.1 Parallelogramm, Dreieck, Trapez, beliebiges Viereck, Vielecke

1. Reelle Zahlen

1.1 Einführung irrationaler Zahlen; Intervallschachtelungen(sehr kurz!)

1.2 Einführung von Quadratwurzeln / Rechnen mit Quadratwurzeln

2. Funktionen

2.1 Quadratische Funktionen / Scheitelpunktform

2.2 Quadratwurzelfunktion / anschaulicher Begriff der Umkehrfunktion

3. Gleichungen / Ungleichungen

3.1 Quadratische Gleichungen(verschiedene Lösungsverfahren ein -
schließlich (p,q)-Formel))

3.2 Linearfaktorzerlegung; Satz von Vieta

3.3 Einfache biquadratische Gleichungen(einige Beispiele)

3.4 Einfache quadratische Ungleichungen (E)

3.5 Einfache Wurzelgleichungen(mit höchstens 2 Wurzeln)

3.6 Einfache Bruchgleichungen und Bruchungleichungen (E)

4. Lehre von den Potenzen

4.1 Potenzen mit natürlichen Zahlen als Exponenten

4.1.1 Begriff der Potenz

4.1.2 Potenzgesetze

4.1.3 Potenzfunktionen(Parabeln)

4.1.4 Monotoniegesetze(kursorisch an konkreten Beispielen)

4.2 Potenzen mit ganzen Zahlen als Exponenten

4.2.1 Definition und Potenzgesetze

4.2.2 Potenzfunktionen(Hyperbeln)

4.3 Potenzen mit rationalen Zahlen als Exponenten

4.3.1 Definition der Potenz und allgemeiner Wurzelbegriff

4.3.2 Potenzgesetze

1. Satzgruppe des Pythagoras

1.1 Satz des Pythagoras; Umkehrsatz(mit Beweis)

1.2 Kathetensatz des Euklid und Höhensatz des Euklid(mit Beweis)

2. Ähnlichkeit

2.1 Erster und zweiter Strahlensatz

2.2 Umkehrung des ersten Strahlensatzes(Andeutung!) (E)

2.3 Begriff der Ähnlichkeit und der zentrischen Streckung(Andeutung) (E)

1. Exponentialfunktionen

1.1 Einführung von Potenzen mit reellen Exponenten(Andeutung!)

1.2 Exponentialfunktionen und einfache Exponentialgleichungen

1.3 Exponentielles Wachstum und andere Wachstumsformen in der
praktischen Anwendung

2. Logarithmusfunktionen

2.1                  Begriff des Logarithmus und Einführung der Logarithmusfunktion
                        als Umkehrfunktion der Exponentialfunktion und einfache Eigen -
                        schaften

2.2 Logarithmusgesetze; logarithmisches Rechnen; "Moduleigenschaft"
zweier verschiedener Logarithmusfunktionen

2.3 Einfache logarithmische Gleichungen (E)

1. Berechnungen am Kreis

1.1 Problematik der Kreisflächenmessung und die Bestimmung der
Zahl p / Bestimmung des Kreisumfangs

1.2 Einführung und Berechnung von sog. Kreisteilen(Kreisbogen, Kreis -
ausschnitt, Bogenmaß usw.)

2. Trigonometrie

2.1 Rechtwinkliges Dreieck

2.1.1 Trigonometrische Verhältnisse im rechtwinkligen Dreieck

2.1.2               Definition und graphische Darstellung aller trigonometrischen Funk -
                        tionen von 0 Grad bis 90 Grad im Koordinatensystem; einfachste
                        Beziehungen bezüglich Winkel und Komplementärwinkel; erste prak -
                        tische Anwendungsprobleme unter Benutzung trigonometrischer
                        Beziehungen(u.a. auch Problemstellungen aus der Flächen- und
                        Raumgeometrie)

2.1.3 Einfache trigonometrische Beziehungen(u.a. trig. Pythagoras) und
spezielle Werte trigonometrischer Funktionen

2.1.4 Einfache trigonometrische Termumformungen

2.2 Beliebiges Dreieck

2.2.1 Trigonometrische Verhältnisse im beliebigen Dreieck

2.2.2               Definition und graphische Darstellung aller trigonometrischen Funk -
                        tionen im Winkel- und Bogenmaß auf ihrem maximalen Definitionsbe -
                        reich(einschließlich Periodizität mit den Perioden 2p bzw. p)

2.2.3 Kursorische Einführung(anschaulich) der Arkusfunktionen(einschließlich
Taschenrechnerbenutzung)

2.2.4 Trigonometrische Beziehungen für Winkel, die größer als 90 Grad
sind(kurze kursorische Behandlung)

2.2.5 Sinussatz und Kosinussatz mit Beweis ; Anwendungsfelder zum
Sinus- und Kosinussatz(u.a. Landvermessungsprobleme usw.)

2.3 Additionstheoreme / Spezielle Funktionenlehre

2.3.1 Additionstheoreme (E)

2.3.2 Sinusschwingungen(Harmonische Schwingungen) (E)

2.3.3 Überlagerung von Schwingungen(Superpositionsprinzip; zusam -
mengesetzte Schwingungen, die nicht harmonisch sind usw.) (E)

3. Raum- und Flächenmessung bei Körpern

3.1 Exemplarische Volumen -und Oberflächenberechnung eines Körpers

Die Unterrichtsinhalte umfassen Schwerpunkte des Lernbereichs Stochastik aus den Jahrgangsstufen 7/8 und 9/10. Der Fall der sog. „Ungeordneten Stichprobe mit Zurücklegen“
(vgl. 2.1) ist von untergeordneter Bedeutung und kann deshalb entfallen.

1. Grundlagen der Wahrscheinlichkeitsrechnung

1.1 Zufallsexperimente

1.2 Laplace-Experimente / Summen-Regel

1.3 Baumdiagramme und Pfadregeln

2. Lottoprobleme

2.1 Urnenmodelle

2.1.1 Geordnete Stichprobe mit Zurücklegen: nk.(Spezialfall des sog.

Zählprinzips)

2.1.2 Geordnete Stichprobe ohne Zurücklegen: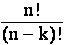

2.1.3 Ungeordnete Stichprobe ohne Zurücklegen(„Ziehen mit einem Griff“):

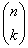
2.1.4 „6 aus 49“ und verwandte Probleme