Curriculum für die Grundkurse in der Sekundarstufe II

Die folgenden schulintern abgesprochenen Unterrichtsinhalte sind obligatorisch; mögliche

"Freiräume" kann jede(r) Kollegin(Kollege) - soweit diese im Rahmen der Oberstufen-

Die für die Jahrgangsstufe 11 für beide Halbjahre aufgelisteten Unterrichtsinhalte sind auch

- wegen der möglichen Durchführung von sog. Parallel-Klausuren - bezüglich der angeführten Reihenfolge verbindlich.

Bezüglich der Durchführung von sog. Parallel-Klausuren sei auf den diesbezüglichen Beschluss

1. Koordinatengeometrie (ca. 10 Wochen)

1.1 Funktionsbegriff + eventuell: anschaulicher Folgenbegriff

1.2 Lineare Funktionen (u.a. verschiedene Formen der Geradengleichung / Parallelität und

Orthogonalität / Länge einer Strecke / falls möglich: Anwendungssituationen)

1.3 Quadratische Funktionen (u.a. Normalparabel / Scheitelpunktform / Nullstellen / aus -

gewählte Extremwertprobleme / Parabelgleichungen: Parabeln symmetrisch zur y-Achse

und zur x-Achse; Steigung der Tangente im Parabelpunkt P / eventuell: Brennpunkt -

eigenschaften der Parabel

Lineare Gleichungssysteme zur Bestimmung der Koeffizienten a, b, c von Parabeln

(Gaußscher Algorithmus)

Anwendungssituationen

1.4 Die Kreisgleichungen / Steigung der Tangente in einem Punkt P des Kreises

Anwendungssituationen

1.5 Falls noch Zeit bleibt: Einige Aufgaben zu Scharen (Geraden, Parabeln, Kreis)

2. Differentialrechnung (ca. 18 - 20 Wochen)

2.1 Begriff der Ableitung einer Funktion an einer Stelle x ₀ (naiver Limesbegriff!) /

Tangentensteigungen und ihre Berechnung / Bestimmung von Tangentenglei -

chungen

Die Ableitungsfunktion f ' / Ableitungen höherer Ordnung

Ableitung der Funktionen mit dem Funktionsterm:

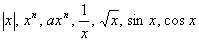und Bestimmung der Tangentengleichung

Faktor -und Summenregel

2.2 Begriff der Änderungsrate / Geschwindigkeit und Beschleunigung in der Physik usw.

(kann natürlich auch schon bei der Einführung des Ableitungsbegriffs besprochen

werden) / Anwendungssituationen

2.3 Falls noch Zeit bleibt: Einige einfache Kurvenscharen.

2.4 Die Analyse von Funktionen mit Hilfe des Ableitungsbegriffs:

Lokale Extrema und Wendepunkte (Unterscheidung von notwendiger und hinrei -

chender Bedingung) / Zusammenhang von Monotonie und Ableitung

Die Vorzeichen-Regel und die sog. "f '' - Regel"

Die Diskussion ganzrationaler Funktionen (einschließlich der Bestimmung von

Nullstellen mittels Polynom-Division; u.a. auch Besprechung des Newton-Ver -

fahrens)

2.5 Falls noch Zeit bleibt: Einige Steckbriefe und einige einfache Kurvenscharen

3. Erweiterungsstoff / Nachträge / Beschreibende Statistik (ca. 10 Wochen)

3.1 Ableitung der Exponential -und Logarithmusfunktion, der Potenzfunktion (ganze und

gebrochene Zahlen im Exponenten)

Produktregel

Falls möglich: Ketten-Regel für einfachste Fälle

3.2 Beschreibende Statistik:

Darstellung statistischer Daten

Verschiedene Mittelwerte

Streuungsmaße und Streuung um den Mittelwert

Lineare Regression (Ausgleichsgeraden / Korrelation)

1. Fortführung der Differentialrechnung (ca. 8 - 10 Wochen)

1.1 Einfachste Fälle von Quotienten -und Ketten-Regel / Ableitung der Tangens -und Ko -

tangensfunktion / Ableitung der Potenzfunktion mit reellen Exponenten

1.2 Kurven-Diskussion an Exponential -und Logarithmusfunktionen /

Untersuchung von Kurvenscharen der bisher behandelten Funktionsklassen

1.3 Ganzrationale Funktionen in Sachzusammenhängen (u.a. Optimierungsprobleme)

2. Integralrechnung (ca. 16 - 17 Wochen)

2.1 Propädeutik zum Begriff des Bestimmten Integrals (Flächenbegriff usw.) /

Begriff der Arbeit / Numerische Bestimmung der Kreisfläche über das

"Rechteckverfahren"; Möglichkeiten der Erweiterung zum Trapezsummen -

verfahren

2.2 Anschauliche Fassung des Begriffs des bestimmten Integrals / Die Integra -

tion der quadratischen Parabel

Ergänzungen und einfachste Lehrsätze zum bestimmten Integral

2.3 Integralfunktion / Stammfunktion / Hauptsatz der Diff. -und Integralrechnung

(bzw. die zwei sog. Fundamentalsätze)

2.4 Unbestimmtes Integral / Grundintegrale / Verfahren der partiellen Integration

2.5 Bestimmung von Flächeninhalten

2.6 Volumina von Rotationskörpern

2.7 Kurvenscharen / Anwendungssituationen

3. Stochastik (Orientierungswissen) (max. 6 Wochen)

3.1 Grundlegende Begriffe und Gesetzmäßigkeiten / relative Häufigkeit und das

Gesetz der großen Zahlen / Pfad-Regeln / Wahrscheinlichkeitsbegriff von

Laplace

3.2 Wahrscheinlichkeitsrechnung im Laplace - Modell: Zählstrategien bzw. kombi -

natorische Methoden und Urnen-Modelle

4. Lineare Algebra / Geometrie (ca. 8 - 9 Wochen)

4.1 Vektorbegriff / Vektoralgebra / Minimale Einführung von Komplanarität und

Kollinearität von Vektoren

4.2 Lineare Gleichungssysteme (LGSe)(u.a. Gaußscher Algorithmus) / Bzgl. LGSe

knappe Einführung des Matrixbegriffs zur symbolisch effektiven Behand -

lung des Gauß-Algorithmus

4.3 Parameterdarstellung der Geraden / Lagebeziehungen von Geraden

Entweder setzt man in 13.1 / 13.2 das Gebiet Lineare Algebra / Geometrie weiter fort oder man be -

handelt in Fortführung des Orientierungswissens Stochastik die Stochastik in 13.1 / 13.2 weiter fort

und betrachtet dann den zum Ende der 12.2 behandelten Teil der Linearen Algebra / Geometrie als

Orientierungswissen für dieses Gebiet. Egal ob man sich nun in 13.1 / 13.2 für eine Fortführung der

Stochastik oder der Linearen Geometrie entscheidet(die Entscheidung ist völlig frei!): Jede dieser

Alternativen erfüllt die Bedingungen der Richtlinien bzgl. der Obligatorik und des Orientierungswissens.

Neben der Einhaltung der Stoffabsprachen für die gesamte J-Stufe 11.1/11.2 ist eine Einhaltung

der Stoffabsprachen (schon wegen möglicher Sitzenbleiber!) für die J-Stufe 12.1/12.2

Die Obligatorik für den Stochastikteil dürfte bzgl. der Stofffülle schwieriger zu bewältigen sein als

Werden neben Analysis beide Gebiete "Lineare Algebra..." und "Stochastik" im Abitur berücksichtigt,

so ist aus den Inhalten eine geeignete Auswahl zu treffen (vgl. Richtlinien, S. 28).

Mögliche Alternativen in Anlehnung an die Richtlinien

1. Alternative 1: Falls Orientierungswissen "Stochastik": ®Fortsetzung

"Lineare Algebra / Geometrie" plus Vertiefungen und Wiederholungen

1.1 Parameterform der Ebenengleichung / Lagebeziehungen von Ebenen und Geraden

1.2 Skalarprodukt und Anwendungen (Orthogonalität, Winkel und Länge von Vektoren)

1.3 Matrizen:

Alternative a): Abbildungsmatrizen / schräge Parallelprojektionen / Matrizenmulti -

plikation als Abbildungsverkettung

Alternative b): Übergangsmatrizen / Materialverflechtung oder stochastische Matrizen /

Matrizenmultiplikation als Verkettung von Übergängen

1.4 Vertiefungen und Wiederholungen

2. Alternative 2: Falls Orientierungswissen "Lineare Algebra / Geo -

metrie": ®Fortsetzung "Stochastik" plus Vertiefungen und Wieder -

holungen

2.1 Bedingte Wahrscheinlichkeit / Unabhängigkeit

2.2 Zufallsgröße und Wahrscheinlichkeitsverteilung / Erwartungswert und Standard -

abweichung

2.3 Die Binomialverteilung

2.4 Beurteilende Statistik:

Alternative a): Testen von Hypothesen

Alternative b): Schätzen von Parametern für binomialverteilte Zufallsgrößen

2.5 Vertiefungen und Wiederholungen